Something better than Bloom? Cuckoo filters.

The annotated paper : here

Structure of this post :

• Introduction to probabilistic data Structures
• How Bloom filters work
• Bloom filters downsides
• Cuckoo filters Intro
• How they work

Probabilistic data structures:

In computer science, high-level problems often require a membership test. So, what is a membership test?

Membership test: This test checks whether the system has seen a given element from a set before.

In such cases, it's enough for the system to know "somewhat" whether a given element was seen before. Along the lines of "Oh, I've definitely not seen that" or "Maybe, I've seen this".

Sort of a definitely not or maybe.

This often suffices as there would be additional data stores that can confirm that maybe into a much more concrete answer, albeit at a higher time cost. Those definitely not help save a lot of time and traffic going to these deterministic data stores.

These data stores that can do this definitely not or maybe are called probabilistic data structures. They work on a probably basis that is right most of the time.

These structures provide both a space and time advantage to the system implementing them. The structure that almost outshines them all is called Bloom filters. If you have spent any amount of time dabbling in Computer Science, I'm almost certain you'd have heard about it. Let's look into Bloom filters next.

Bloom filters

Bloom filters are probabilistic data structures. They don't store the item itself but are a way to identify if the item was seen previously.

They have a bitarray of size n [In this case it's 15] representing these items of a set. Each item, during insertion, is passed through a series of hash functions that set some subset of the bits of the same bitarray to 1. Each of the hash functions may overlap each other for the same item and different items. It looks something like this :

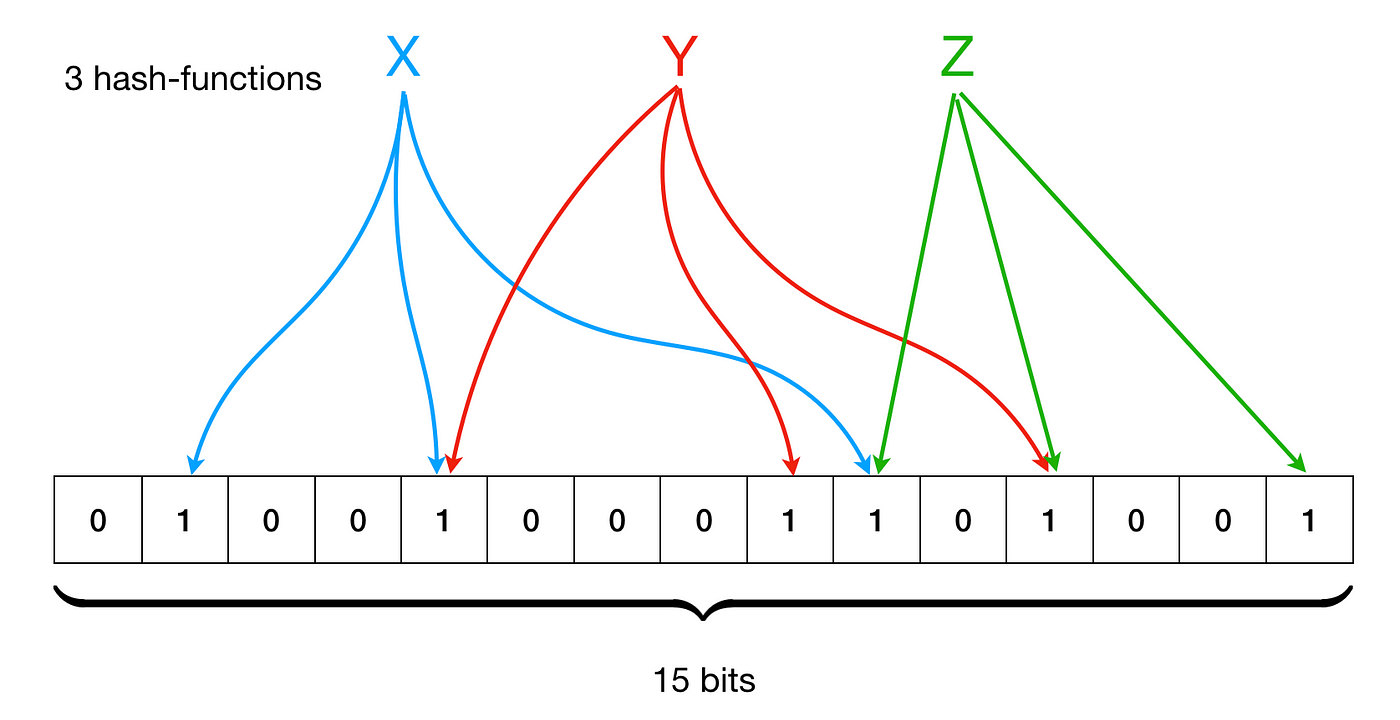
While we check the membership of a given item, we send the item under check through the same hash functions and check if each of the positions given by the hash functions as output is set to 1.

If any one of the positions is 0, we return false (we are sure we haven't seen this item). If all the positions are 1, we "might" have seen this before.

This ambiguity enters the equations as 2 items could have the same output from all the hash functions (a hash collision to say). So how much space did we save by using bloom filters for the membership test instead of the full set?

Allowing for false positive rates of e, the theoretical minimum will be log2(e) [No. of bits required to represent an item of a set with error e - m]. But through some math, we get at 1.44 x log2(e). If you are interested in the math, you can find my notes here.

Space equations of bloom filters It also has some useful equations for finding the optimal number of hash functions - k If you plan to use bloom filters for anything serious, you need this math!

But as a summary, 1.44 x log2(e) tells us that bloom filters take up 1.44 times (44%) the theoretical minimum.

Furthermore, bloom filters cannot "delete" the membership of an item from the bit array, again, due to the possible clashes of bits for items with the same hash outputs...or even different hash outputs, as a single bit in the bitarray can be shared among multiple different items.

Deleting even a single bit will lead to a huge rise in false negatives which is unacceptable for a probabilistic data structure. The only way to delete the membership of an item is to rebuild the bitarray.

Cuckoo filters promise space usage very close to the theoretical minimum and allow the deleting of membership of items seen previously.

Cuckoo filters

In this post, we only see how cuckoo filters work. Not the math behind it. Although the paper does a good job of explaining it if you need it!

Cuckoo filters, like bloom filters, also don't store the item itself. But unlike bloom filters, they store a unique fingerprint of the item. This fingerprint is a hash of the item itself. Cuckoo filters, very early on in its paper, indicate this :

To make a filter more space efficient, you need to increase its space occupancy. This can be done by giving items more than one place to be stored.

Cuckoo filters do this, by a concept called partial-key hashing. Furthermore, to support deleting, the filter must be able to get the position of where the fingerprint of the said item is stored. Yet again, partial-key hashing solves this. (Many, partial-key hashing sounds quite magical).

Structure of cuckoo filters:

• The basic unit of storage in cuckoo filters is called an entry.

Each entry stores one fingerprint.

• The table consists of an array of buckets, where each bucket can store multiple entries.

Cuckoo filters work similarly to cuckoo hashing, where each item is stored in one place. When inserting an item, the place for it is determined by hash(item). If the said place is already occupied, the item in that place is kicked out and reinserted into its alternative place. This continues until we find a free spot or, we reach a maximum number of kicks. But cuckoo hashing stores the original item, to pass it into a second hash function to find its alternative place. Cuckoo filters don't do this. (You can sort of see how we achieve high occupancy in cuckoo filters)

Insert algorithm:

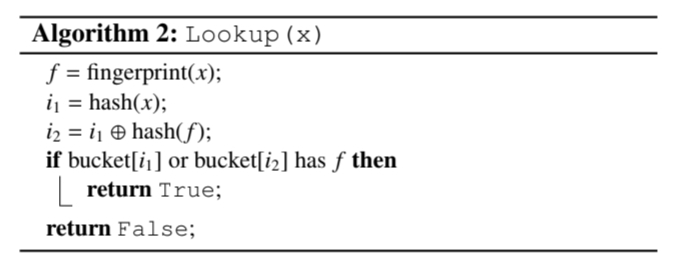
We now get introduced to the partial-key hashing. For a given item x, our hashing calculates the two possible buckets in the table as :

h1(x) = hash(x) 
h2(x) = h1(x) XOR hash(fingerprint(x))

The XOR operation is crucial in the above hashes, as h1 can be determined using h2 and the fingerprint of the item. So, to displace a key, originally in bucket i (doesn't matter if "i" is h1 or h2), we can find the alternate position (bucket j). By using the current bucket i and its fingerprint :

j = i XOR hash(fingerprint(x))

This way, if the current bucket is h1, we get h2 as j. If the current bucket is h2, we get h1 as j. SO BEAUTIFUL!

Insertion, hence uses only the information already present in the table. The shrewd might notice that the fingerprint doesn't have to be hashed to find h1 and h2, this two-way function would have worked just as fine without it. However, the authors of the paper have a reason for this.

The fingerprint is hashed before XOR with the current bucket index to help distribute the item evenly across the table. If the fingerprint was not hashed, like i XOR fingerprint(item_to_be_displaced) it would lie very close to the insertion item x as they have similar hashes and hence are trying to enter the same table. This would lead to uneven filling up of the table.

Lookup and Delete:

Lookup and delete are rather easy. For lookup, find the position of the fingerprint using the same hash functions as insertion. If the fingerprint is found, we can be sure that the item was seen before. If not, just check the alternate position as well.

For delete, we find the position of the fingerprint using the same hash functions as lookup. If the fingerprint is found in the bucket, we can delete it. If not, we check the alternate position. Cuckoo filters do have a problem with deleting. For safely deleting an item x the item must have been seen before. Cuckoo filters might sometimes delete the fingerprint of an item that was never seen before (Due to conflicting fingerprints).

With this, I conclude this post.

Fin.

---