Linearizability testing

100% based off of this blog

Linearizability is a concept of Distributed systems. Non-determinsim makes testing systems very hard. Before a system can be tested, we need to first define its correctness:

Correctness of linearizable systems :

In our case, let's consider a KV store. In a linear sequence first.

Two operations : GET(key) PUT(key, value)

It's easy to define how this KV store should behave in a linear sequence. But say in such a given scenario, it's not defined :

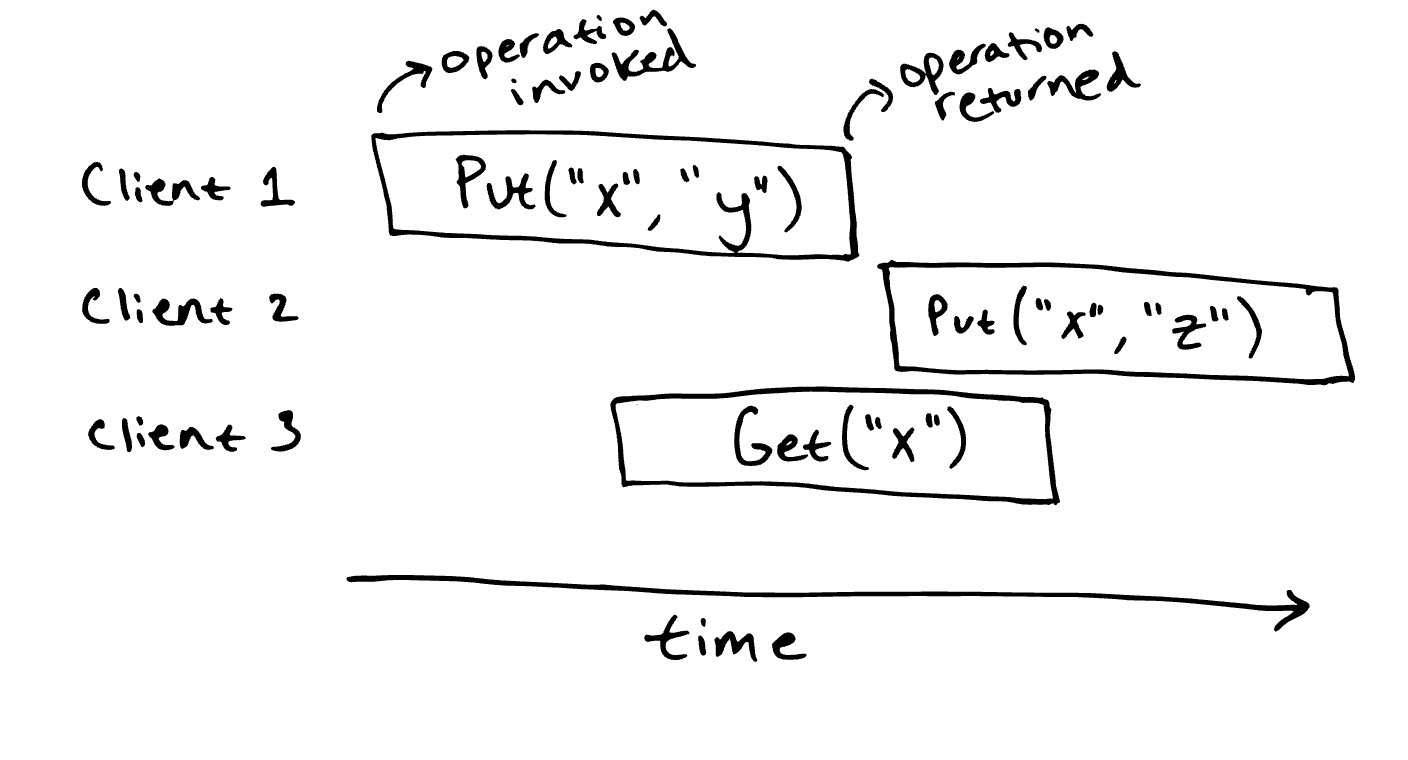
We formally specify correctness for concurrent operations based on a sequential specification using a consistency model known as linearizability. In a linearizable system, every operation appears to execute atomically and instantaneously at some point between the invocation and response.

So in such a case, this would be considered a linearizable system :

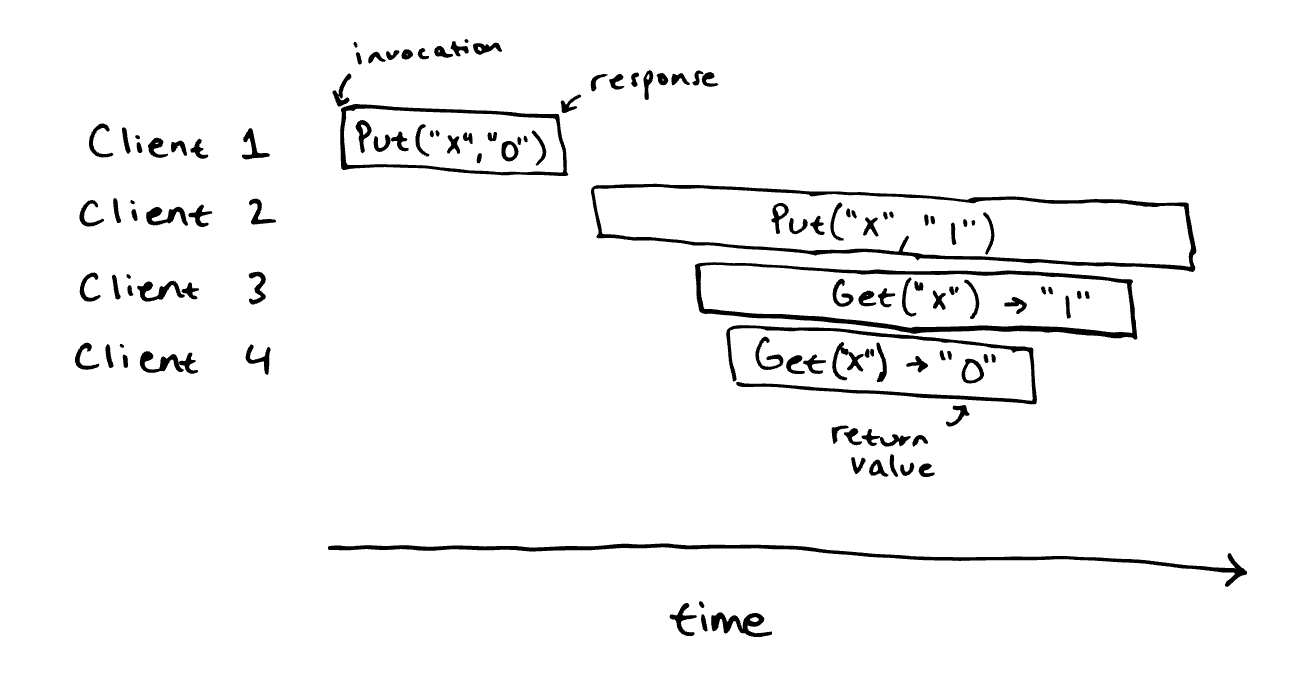
Why? As we can point to the "atomic posistion" the operation took place, and that place is between its invocation and its response.

In the other hand, this is not linearizable :

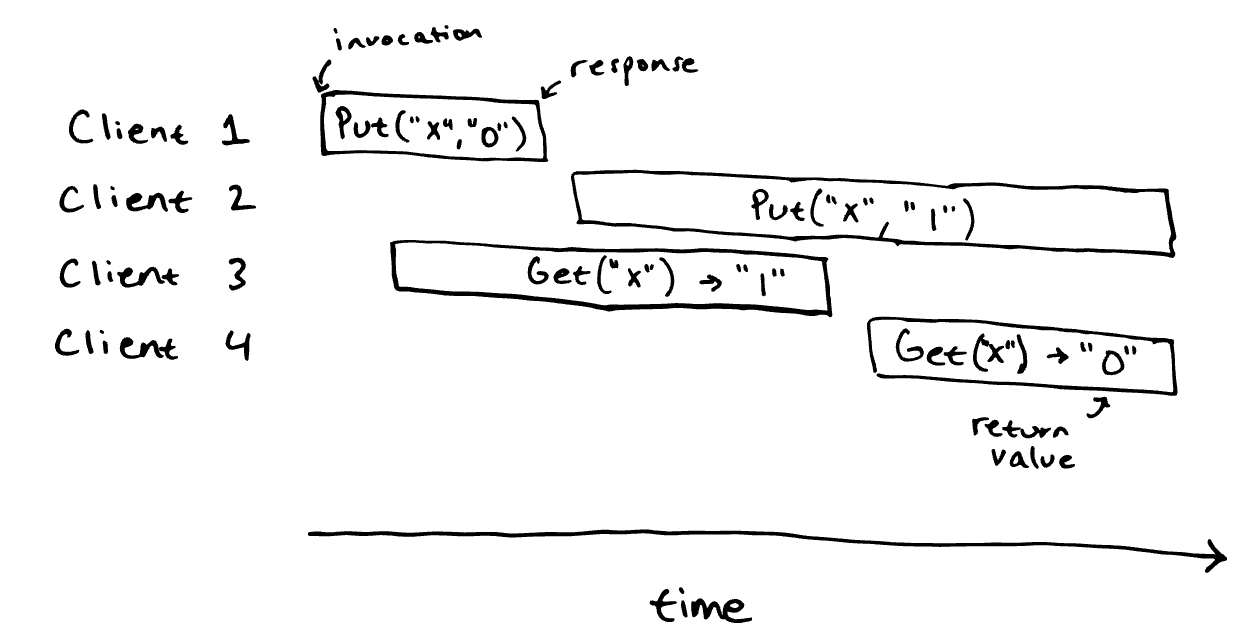
Testing

We now know what "correctness" is in a linearizable system, how do we test it?

We could simulate full networks, latencies, failures, partitions. This is what Jepsen as a testing framework does (You should check it out, its really cool).

But this test's the system as a whole, not particular operations. Hence, the longer you test with varying condition, the more confidence in your system, obviously...this is time-consuming.

We could try ad-hoc testing

ad-hoc testing

This is where we are simply testing it like any other code. "ad-hoc" means, "for the requirement".

We could do something like this :

for client_id = 0..10 {
    spawn thread {
        for i = 0..1000 {
            value = rand()
            kvstore.put(client_id, value)
            assert(kvstore.get(client_id) == value)
        }
    }
}
wait for threads

This ensures that for a given thread, if the put operation is finished (that is the store is stating that it has atomically at some point executed it), we are able to read it.

It's good, but not thorough. As each thread is operating on its own key. There can be non linearisable systems that pass this test.

A better test would be to have concurrent threads write to the same key, and assert for an output. But what is the output we should assert for....well that gets tricky.

Linearizability checker

We need to store all the "successful" acked operations and check if each operation satisfies the linearizable correctness. This would be what we call linearizablity checker!

A linearizability checker takes a sequence of concurrent outputs and checks them

Turns out, linearizability checking is a NP-Hard problem.

NP Problems :

NP Problems are those that can be solved by Non-deterministic computers in polynomial time.

Polynomial time is when the complexity of a solution is a function of polynomial expression

As an example (To define NP) source:

Let us consider an example to better understand the NP class. Suppose there is a company having a total of 1000 employees having unique employee IDs. Assume that there are 200 rooms available for them. A selection of 200 employees must be paired together, but the CEO of the company has the data of some employees who can’t work in the same room due to personal reasons. This is an example of an **NP **problem. Since it is easy to check if the given choice of 200 employees proposed by a coworker is satisfactory or not i.e. no pair taken from the coworker list appears on the list given by the CEO. But generating such a list from scratch seems to be so hard as to be completely impractical.

It indicates that if someone can provide us with the solution to the problem, we can find the correct and incorrect pair in polynomial time. Thus, for the NP class problem, the answer is possible, which can be calculated in polynomial time.

What is NP-Complete problem now?

Subset of NP problems, where all NP problems can be converted to this subset in polynomial time. (I'm keeping it simple).

What is NP-Hard problem now?

Set (NOT A SUBSET) of problem, where all NP-Complete problems can be converted to this set in polynomial time.

So, if some absolute giga chad genius, find the solution to one NP-hard problem, it's over for us all.

Despite linearizabilty checking being a NP-hard problem, its still an effective way to test systems for a small log of concurrent operation logs. We have testers like :

• Jepsen
• Knoss
• Procupine

That do this exact thing. Linearizability testing is generally considered far better than simple ad-hoc testing.